I often notice that many students of programming do not understand the actual meaning of regular expressions. And I have seen online tutorials and even books that do not explain properly what regular expressions are.
Most books and tutorials do not explain the actual theory behind regular expressions. They are not really a tool or just fancy wildcards. A finite state machine (FSM) is the actual tools behind every regular expression and a regular expressions is used to define such an FSM. Learning regular expressions without the knowledge of FSMs is like learning to swim without water.
It’s probably because wildcards (most often an asterisk: *) are used in most search functions and so regular expressions just seem like very advanced wildcards. That’s basically true, but there is a much more accurate formal definition.
Another problem is that very unrealistic examples are used in tutorials. You often find examples of code that should validate an email-address. But a regular expression can’t know if the address is truly valid. And they usually don’t even use the standard expression defined by W3C:
This is much too complex to learn regular expressions. And you’d just use the standard expression, so why start with that?
What a regular expression really is
It’s just a word. Each regular expression is a sequence of characters. Another word for that is word. A word is a sequence of characters from a predefined alphabet, which is a nonempty set of characters. A regular expression can be empty (zero characters long), but it is finite.
- Alphabet
- A set of symbols.
Example:{' ','A','B','C',...,'Z','a','b','c',...,'z'} - Word
- A sequence of symbols.
Example:"Hello World", "xRbWkg", "" - Language
- A set of words.
Example:{"","Java","Programming","Regular Expressions"} - Regular Expression
- A word that defines a finite state machines, which represents a regular language.
Example:"a{1,2}B?"
ℒ("a{1,2}B?") = {"a","aa","aB","aaB"}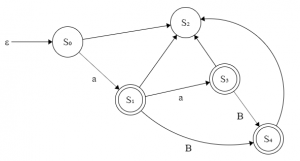
To decide whether a word is part of the language or not you check each character and see if the the FSM defined by the regular expression accepts the word when you processed the last character. The machine used to parse the input is a finite state machine (FSM). And the regular expression is just a formal definition of that FSM. The accepted states have two border lines, other states are not accepted. The input "aaa" goes S0, S1, S3, S2 and is therefore not accepted. Just "aa" goes S0, S1, S3, which is accepted.
So a regular expression defines a FSM. And a FSM accepts or rejects words. The set of accepted words is a language. It’s the language defined by the regular expression.
This can be used to check if a word (a “string”) is part of the language. It is if the FSM accepts the complete sequence of characters. But substrings are words too. You can use a regular expression to search for substrings, but that’s just one possible use.
What a regular expression really does
It defines a language. A language is a set of words.
In the above example (see box) I use ℒ as a function that takes a regular expression and returns a language (set of all accepted words). This only works in theory, because a language can be of infinite cardinality. |ℒ("a+")| = ∞
So basically a regular expression does the same as a dictionary would for a natural language. You could have a regular expression like this:"(a|about|above|across|act|active|activity|add)", which would accept some of the first words in the English language. But that’s just a list. A regular expression can also describe how letters can form words. Such as "a+" for all words that contain the symbol 'a' at least once and nothing else.
An English dictionary might contain an entry “non-“. It means that for every adverb you can create a new adverb by putting “non” in front of it. “heinous” becomes “nonheinous” and “nonheinous” becomes “nonnonheinous“. That’s how a language can technically contain infinite words.
What this means
If you collect all regular expressions (they are all words) you get a set of words. And a set of words is a language. We have learned that each regular expressions defines a language.
So regular expressions are a language of words that each define a regular language. It’s a language of languages.
What it can’t do
To define a set of words starting with “non” you could use this RE:/(non)+\w+/
But you can’t know if something is an adverb. That would be semantics. So it also accepts “none” and “nonplus”. Those are English words, but not created by the “non”+adverb-rule.
Not all languages are regular. Some are context-free, context-sensitive or recursively enumerable. A regular language is one where each new letter can be processed and no “memory” is needed other than the current state. This is less than you could do by executing machine code.
What you should learn first
So the only thing you really need to learn are finite state machines. And then regular expressions are just another way to describe them. But to truly understand FSMs you need to have some basic knowledge on other topics. I recommend leaning these topics first:
- basic programming
- set theory
- graphs
- propositional logic
- state machines
At my school all these topics are thought at a course called “discrete math” (two semesters).
Why you should learn state machines first
I found this on the internet:

It’s a perfect example on how you should not learn about regular expressions. And that’s not just because the last example is complete nonsense. $[0-9] wouldn’t match anything. The wording on the other examples is also not precise enough: * doesn’t only work with characters. A class doesn’t match “anything”. It matches a single character unless there is a quantifier. When ^ is used outside a character class it is not used for negation.
The major problem here is that it doesn’t explain at all how regular expressions define finite state machines and a regular languages or how they are to be used. I know text books are expensive, but can you really affort wasting your time on such rubbish like the image above?
Why regular expressions are often not the right choice
Not only do many not understand what regular expressions really are, they also don’t know the limitations and what better alternatives exist for certain problems. Using a regular expression only makes sense when it’s actually better than all alternatives.
Not every language is regular
Some formal languages can’t be described by a FSM. Usually you will just write some code that will decide whether a word should be accepted or not. Code written in any Turing-complete language can do more than a regular expression.
Even if some language is regular now you can’t always be certain that this won’t change in the future. Requirements change all the time.
Hard to maintain
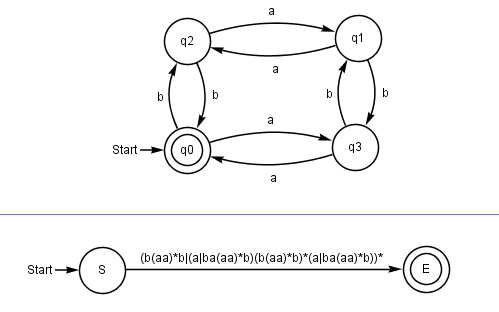
Code to do the same might be simpler and easier to maintain. You can’t add comments to regular expressions in any useful way. The state machine for all words that consists of as and bs, both of even number, is rather simple. But the regular expression for it is insanely complex. Still there are some books that actually use this as an example. Here’s the FSM (top) and the regular expression derived from it (below):
Performance
Regular expressions can be precompiled, but a state machine is often faster. In many cases an expression for the language is too complex, so multiple languages are defined and only the intersection of all languages is used. This takes longer than one FSM that defines the actual language. The language of as and bs of even numbers is again a good example.
Security
Even security is a problem when it comes to regular expressions. There’s a thing called regular expression denial of service. But a more basic problem is that regular expressions are hard to understand and a seemingly small error might lead to catastrophic problems. In some cases regular expressions are used to search user defined terms in databases. When user input is used to create regular expressions it might lead to serious security risks.
When they should be used
Whenever a FSM is needed and a regular expression is more convenient than actually writing the code.
Links:
- http://regex101.com – Interactive Online Regex Tester
- http://regexcrossword.com – Fantastic World of nerdy Regex Fun
- http://www.regular-expressions.info – The Premier website about Regular Expressions
- http://www.educ.ethz.ch/unt/um/inf/ti/exorciser – Exorciser: Theoretische Informatik ETH
You have written very well .